Srinivasa Ramanujan’s formulas for pi are fundamentally linked to modern high-energy physics, specifically emerging in the mathematics of logarithmic conformal field theories (LCFTs). These theories describe physical systems that exhibit scale invariance, such as turbulence and phenomena related to black holes. 

The Link to Modern Physics

Physicists at the Indian Institute of Science (IISc), specifically Professor Aninda Sinha and Faizan Bhat, discovered a surprising connection between the purely mathematical formulas developed by Ramanujan in 1914 and fundamental physics. 

• Conformal Field Theories (CFTs):Ramanujan’s formulas naturally arise within a broad class of theories called conformal field theories, which are used to describe systems where patterns repeat at different magnifications (scale invariance).
• Physical Phenomena: These mathematical structures are particularly relevant to specific, complex physical scenarios, including:
  • Turbulence
  • Percolation (e.g., how a fluid moves through a porous material)
  • Certain aspects of black holes and cosmological models
• Computational Efficiency: The inherent efficiency of Ramanujan’s series for calculating pi, where each term adds roughly eight decimal places of accuracy, mirrors a novel, faster way to perform calculations in these complex physics theories. 

Yes, there is a recently discovered link between Srinivasa Ramanujan’s formulas for calculating pi (\pi) and modern high-energy physics theories.  

Physicists have found that the mathematical structure underlying Ramanujan’s century-old, highly efficient series for 1/\pi (like the one below) naturally emerges in theoretical models describing complex physical systems. 

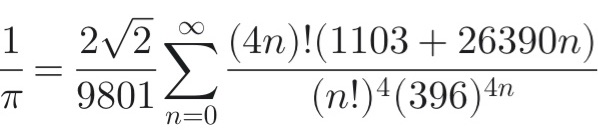
⚡️ Practical Application in Physics

The discovery provides a practical tool for physicists:

• Faster Calculations: Just as Ramanujan’s series provided an extremely efficient way to compute \pi to trillions of digits, the mathematical structure they share with CFTs can be used to efficiently calculate certain quantities within these modern physics theories. This can make complex, time-consuming calculations faster and more manageable.  

• Anticipation of Structure: The link suggests that Ramanujan, working in pure mathematics in the early 20th century, inadvertently formulated structures that are now central to understanding fundamental physical phenomena in the universe today.  

• 
  The Chudnovsky algorithm is the most famous example of how Ramanujan’s work translates into modern, record-breaking computation.
  💻 The Chudnovsky Algorithm
  The Chudnovsky algorithm, developed by David and Gregory Chudnovsky in the 1980s, is the formula most often used by supercomputers to calculate \pi to trillions of digits. It is directly based on the structure of Ramanujan’s series.
  🚀 Key to its Efficiency
  The incredible speed and efficiency of the Chudnovsky algorithm stem from two main factors:
  1. Extremely Fast Convergence (Ramanujan’s Formula):
  • The formula is a Ramanujan-Sato series, which is a type of infinite series that converges very rapidly.
  • Every single term added to the summation in the Chudnovsky algorithm typically adds about 14 to 15 new, correct decimal digits to \pi. This is much faster than earlier methods, where you might need thousands of terms for just a few digits.
  • The core series used is:
  
  
  2. Binary Splitting (Computational Optimization):
  • To handle the massive numbers and factorials in the formula, the algorithm uses a technique called binary splitting.
  • This technique is an optimization that converts the sum of many individual fractions into one giant fraction. This means the computer only has to perform one single division at the very end of the calculation, which is a huge time-saver for calculations involving trillions of digits.
  🏆 World Record Calculations
  The Chudnovsky algorithm has been the basis for nearly all \pi calculation world records since its publication, including the most recent ones that have exceeded 100 trillion digits.
  The reason this video is relevant is that it features one of the Chudnovsky brothers, who developed the algorithm that is now the world standard for calculating \pi based on Ramanujan’s formulas.
  This World Record took YEARS (and a Million dollars..)

Ramanujam life story and achievements

Srinivasa Ramanujan (1887–1920) is widely regarded as one of the greatest mathematicians in history. His life was a remarkable journey of self-taught genius, enduring poverty, and a deeply fruitful collaboration that resulted in groundbreaking mathematical achievements.

📖 Life Story of Ramanujan

Early Life and Struggle (1887–1913)

• Birth and Early Genius: Born on December 22, 1887, in Erode, Tamil Nadu, India, into a poor Brahmin family. He displayed an extraordinary, intuitive grasp of mathematics from a young age.

• Self-Taught Master: His mathematical education was largely self-directed. At age 16, he came across G. S. Carr’s Synopsis of Elementary Results in Pure and Applied Mathematics, a collection of thousands of theorems. This book ignited his genius and served as the foundation for his own original research.

• Academic Hardship: Despite his brilliance in mathematics, he repeatedly failed in non-mathematical subjects (like English and Physiology) in college. This led to him losing his scholarship and dropping out, forcing him into years of poverty and struggle for employment.

• The Notebooks: During this time, while struggling to find work, he filled three famous “Notebooks” with thousands of original theorems and formulas, often without proof.

The Hardy-Ramanujan Collaboration (1913–1919)

• The Letter to Hardy: In 1913, Ramanujan, desperate for an audience who could understand his work, wrote a letter containing 120 of his theorems to the renowned English mathematician G. H. Hardy at the University of Cambridge.

• The Discovery: Hardy, initially skeptical, recognized the work as extraordinary, containing both known deep results and completely new, groundbreaking theorems. He famously stated that discovering Ramanujan was his greatest contribution to mathematics.

• Journey to England: Hardy arranged for Ramanujan to travel to Cambridge in 1914. This five-year collaboration was highly productive, leading to numerous joint papers and expanded mathematical horizons for both men.

• Recognition: In 1918, Ramanujan was elected a Fellow of the Royal Society (FRS)—one of the youngest in history and only the second Indian to be so honored. He was also elected a Fellow of Trinity College, Cambridge.

Return and Final Years (1919–1920)

• Illness and Return: Ramanujan, a strict vegetarian, faced severe dietary and health challenges in the cold English climate. His health deteriorated (likely due to a combination of tuberculosis and severe vitamin deficiency), and he returned to India in 1919.

• Final Masterpiece: Even on his deathbed, he continued to produce profound work, notably concerning the Mock Theta Functions, which are still an active area of research today.

• Death: He passed away tragically young on April 26, 1920, at the age of 32.

In total, Ramanujan independently compiled nearly 3,900 results, most of which have been proven correct, with many still leading to new mathematical discoveries today.

Please like subscribe comment your precious comment on universe discoveries

Full article source google